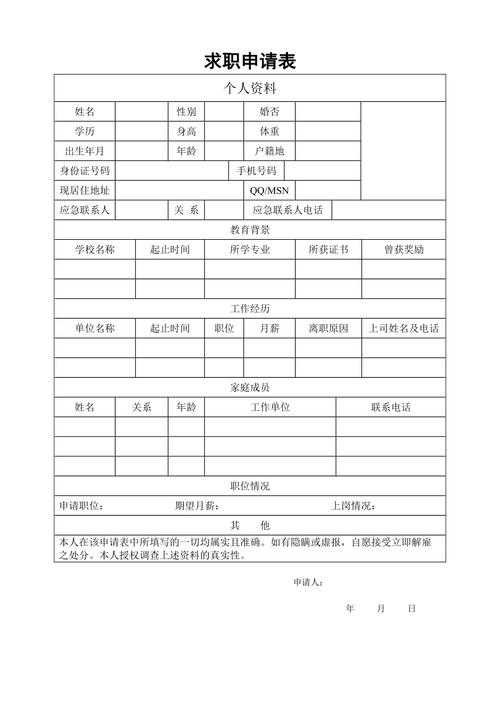
两点间距离公式是∣AB∣=√[(x1-x2)²+(y1-y2)²]。
两点间距离公式叙述了点和点之间距离的关系。
设两个点A、B以及坐标分别为:A(X1,Y1)、B(X2,Y2)则A和B两点之间的距离为:∣AB∣=√[(x1-x2)²+(y1-y2)²]。两点距离公式是常用于函数图形内求两点之间距离、求点的坐标的基本公式,是距离公式之一。
两点间距离公式推论:
已知AB两点坐标为A(x1,y1),B(x2,y2)。
过A做一直线与X轴平行,过B做一直线与Y轴平行,两直线交点为C。
则AC垂直于BC(因为X轴垂直于Y轴)
则三角形ACB为直角三角形
由勾股定理得
AB^2=AC^2+BC^2
故AB=根号下AC^2+BC^2,即两点间距离公式。
点到直线的距离:
直线Ax+By+C=0 坐标(x0,y0)那么这点到这直线的距离就为:d=│Ax0+By0+C│/根号(A^2+B^2)。
公式描述:
公式中的直线方程为Ax+By+C=0,点P的坐标为(x0,y0)。
连接直线外一点与直线上各点的所有线段中,垂线段最短,这条垂线段的长度,叫做点到直线的距离。
设A(x1,y1)、B(x2,y2),则A、B两点的距离公式是(x1-x2)^2+(y1-y2)^2再开方。