雷锋网 AI 科技评论按:「熵」大概是统计学、信息学里最让初学者愁肠百结的基本概念之一。我们都知道熵可以用来描述含有的信息丰富程度的多少,但是具体是怎么回事呢?这篇文章中雷锋网 AI 科技评论将带大家重新系统认识一下「熵」倒是在讲什么。

假设你在医生办公室中与三个等待的病人交流。三个病人都刚刚完成药物测试,他们面临着两种可能的结果:患病或者未患病。假设这三个病人都充满好奇心而且数学好。他们提前各自研究得到了自己患病的风险,并且想通过这些来确认自己的诊断结果。
病人 A 知道他自己有 95% 的可能会患病。对于病人 B,患病概率为 30%,病人 C 的患病未患病的概率都为 50%。

病房中的不确定性
首先我们专注于一个简单的问题。在其他条件都相同的情况下,这三个病人中的哪个面临着最大的不确定性?
这个问题的答案是显而易见的,病人 C。他所面临的是在这种情况下可能呢存在的最大程度的不确定性:就像医疗版本的抛硬币试验一样。
对于病人 A 来说,虽然他的情况不容乐观,但是至少他对于是否患病这个问题有最小的不确定性。对于病人 B,他的不确定性在病人 A 和病人 C 之间。
这就是为什么要引入熵这个概念的原因:描述一个状况下的不确定性为在xx和xx之间,在日常生活环境下这种精细程度可能足够了,但是对于机器学习任务来说,这种描述太宽泛了。
不确定性度量
熵允许我们对于生活中的一个重要问题:事情最终会发展到什么样的结果,进行精确度量和计算。
换种说法,熵是一种不确定性的度量。
在本篇文章中,熵都是指代香农熵(Shannon entropy)。其实还有几种其他类型的熵,但是在自然语言处理或者机器学习领域中,我们提到的熵都是香农熵。
所以在没有特意说明的情况下,下面就是熵的公式。对于事件X,有n种可能结果,且概率分别为p_1, ... p_n,公式为:
基本性质
如果你是第一次看到这个公式,你可能会提出一个问题:为什么要用对数?为什么这个公式就能够度量不确定性?当然,还有为什么要用字母H来表示熵?(表面上这个英文字母H是从希腊大写字母Eta上演变过来的,但实际上为什么采用了字母H来表示,还是有一段复杂的历史的,感兴趣的可以看这个问题:Why use H for entropy?)
对于很多情况下的问题,我认为从以下两点切入是很好的选择:(1)我所面对的这个数学结构有那些理想的属性?(2)是否有其他结构也能够满足所有这些理想的属性?
对于香农熵作为不确定性的度量来说,这两个问题的答案分别是:(1)很多,(2)没有。
我们来一个一个看我们希望熵的公式应该具有哪些性质。
基本性质1:均匀分布具有最大的不确定性
如果你的目标是减小不确定性,那么一定要远离均匀概率分布。
简单回顾一下概率分布:概率分布是一个函数,对于每个可能的结果都有一个概率,且所有的概率相加等于 1。当所有可能的结果具有相同的可能性时,该分布为均匀分布。例如:抛硬币实验(50% 和 50% 的概率), 均匀的骰子(每个面朝上的概率都为六分之一)。

均匀分布具有最大的熵
一个好的不确定性度量会在均匀分布时达到最大的值。熵满足这个要求。给定 n 个可能的结果,最大的熵在所有结果的概率相同时得到。

下面是对于伯努利试验中熵的图像。(伯努利试验有两种可能的结果:p和1-p):

在伯努利试验中,当p=0.5时,熵达到最大
基本性质2:对于独立事件,不确定性是可加的
假设 A 和 B 是独立事件。换句话讲,知道事件 A 的结果并不会丝毫影响 B 的结果。
关于这两个事件的不确定性应该是两个事件单独的不确定性的和,这也是我们希望熵的公式应该具备的性质。
对于独立事件,不确定性是可加的
让我们使用抛两个硬币的试验作为例子来使这个概念更加具体。我们既可以两个硬币同时抛,也可以先抛一个硬币再抛另一个硬币。在两种情况下,不确定性是相同的。
考虑两个特殊的硬币,第一个硬币正面朝上 (H, Head) 的概率为80%,背面朝上 (T, Tail) 的概率为 20%。另一个硬币的正面朝上和反面朝上的概率分别为 60% 和 40%。如果我们同事抛两枚硬币,那么有四种可能:正正,正反,反正,反反。对应的概率分别为[0.48, 0.32, 0.12, 0.08]。

两个独立事件的联合熵等于独立事件的熵的和
将这些概率带入到熵的公式中,我们能够看到:
就跟我们设想的一样,两个独立事件的联合熵等于各个独立事件的熵的和。
基本性质3:加入发生概率为0的结果并不会有影响
假设有一个游戏,获胜条件如下:(a)只要#1号结果出现,你就赢了。(b)你可以在两个概率分布 A 和 B 中选一个进行游戏。分布 A 有两种可能,#1号结果为 80% 概率,#2号结果为 20% 概率。分布 B 有三种结果,#1号结果80%,#2号结果20%,#3号结果0%.

增加第三个概率为0的结果并不会有什么不同
给定 A 和 B 两个选择,你会选哪个?可能正确的反应应该是耸耸肩或白个眼。第三个结果的加入并没有增加或减少这个游戏的不确定性。谁关心到底是用A还是B呀,因为用哪个都是一样的。
熵的公式也满足这个性质:
即,增加一个概率为0的结果,并不会影响对于不确定性的度量。
基本性质4:不确定性的度量应该是连续的
最后一个基本性质是连续性。
连续性的最直观的解释就是没有断开或者空洞。更精确的解释是:输出(在我们的场景下是不确定性)中任意小的变化,都可以由输入(概率)中足够小的变化得到。
对数函数在定义域上每个点都是连续的。在子集上有限数量函数的和和乘积也是连续的。由此可能得出熵函数也是连续的。
唯一性定理
Khinchin(1957)证明,满足上述四种基本属性的唯一函数族具有如下形式:
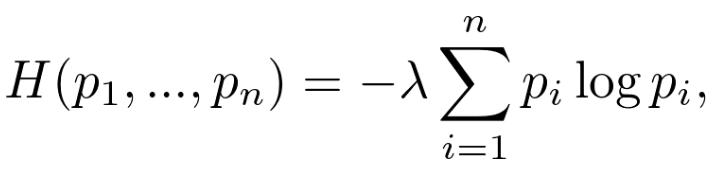
其中λ是正常数。Khinchin称之为唯一性定理。将λ设为1,并使用以2为底的对数就得到了香农熵。
重申一下,使用熵作为不确定性度量是因为它具有我们期望的属性,并且是从满足上面提到的四个属性的函数族中做出的很自然的选择。
其他属性
除了上述用于Khinchin的唯一性定理中的四个基本属性,熵还具有一些其他的性质,下面就介绍其中的一些。
性质5:具有更多可能结果的均匀分布有更大的不确定性
比如你可以在抛硬币试验和抛骰子试验中做出一个选择,如果硬币正面朝上或者骰子1那面朝上就算赢。你会选择那个试验?如果你想最大化收入,肯定会选择硬币。如果只是想体验下不确定性,那可能就会选骰子。

随着等概率结果的数量的增加,不确定性的度量也应该增加。
这正是熵所做的:H(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)> H(0.5, 0.5)
一般来说,L(k)为具有K个结果的均匀分布的熵,我们能够得到:
对于m>n,有
性质6:事件拥有非负的不确定性
你知道什么是负的不确定性吗?反正我也不知道。
对于一个用户友好的不确定性度量来说,无论输入是什么,应该总会返回一个非负的结果。
熵的公式同样满足这个性质,我们来看一下公式:

概率是定义在0-1的范围内的,因此是非负的。所以概率的对数是负的。概率乘概率的对数不会改变符号。因此求和之后应该是负的,最终负负得正。所以对于所有的输入,熵都是非负的。
性质7:有确定结果的事件具有0不确定性
假设你拥有一个魔法硬币,无论你怎么抛,硬币总是正面朝上。

你会怎么量化这个魔法硬币的不确定性,或者其他情况下有确定结果的事件的不确定性?这中情况下就没有不确定性,所以结果也很自然,不确定性为0。
熵的定义也满足这个性质。
假设结果i一定会发生,即p_i=1, 所以H(X)为:
即,确定事件的熵为0。
性质8:调转参数顺序没有影响
这是另一个显而易见的理想性质。考虑两种情况,第一个,抛硬币正面朝上的概率和背面朝上的概率分别为80%和20%。第二个情况里概率正好相反:正面朝上和背面朝上的概率分别为20%和80%。

两种抛硬币试验都有相同的熵,即H(0.8, 0.2) = H(0.2, 0.8)。
更通用的形式,对于个结果的试验,我们有:
实际上这对于有任何数量结果的试验都适用。我们可以以任意的方式调整参数的顺序,而所有的结果都是一样的。
总结
回顾一下,香农熵是一种不确定性的度量。
它被广泛的适用,因为它满足了我们想要的一些标准(同时也是因为我们生活中充满了不确定性)。唯一性定理告诉我们,只有一个函数族具有我们想要的四种基本性质。香农熵是这个函数族的一个很自然的选择。
熵的性质有(1)对于均匀分布有最大的熵;(2)对于独立事件熵是可加的;(3)具有非零概率的结果数量增加,熵也会增加;(4)连续性;(5)非负性;(6)确定事件的熵为0;(7)参数排列不变性。
via TowardsDatascience,雷锋网 AI 科技评论编译
,











