多年前,网上流传着一个经典的段子
“小明,听说你大学的专业是流体力学?”
“是的,领导。”
“那好,去帮我倒杯水。”
“领导,请你尊重这门专业,流体力学是……”
“请你谈谈非等熵的稳态可压磁流体力学方程在持续等离子体约束受控热核聚变中的应用。”
“领导,饮水机在哪?”
哭笑不得之际,我们不禁要问,流体力学到底是干啥的?难道流体力学专业的娃儿只能给领导端茶倒水吗?
作为力学的重要分支,流体力学主要研究在各种力的作用下,流体的状态、运动规律以及流体与外界的相互作用。地球人对流体都不陌生,我们呼吸的空气、喝的水,都是流体。那么流体力学研究中又是如何分类流体的呢?
理想流体 VS 实际流体
自然界中的流体都有粘性,统称为粘性流体或实际流体。比如我们搅拌蜂蜜时会感受到粘滞的作用,而飞机飞行所受的阻力也很大程度上来源于空气的粘性。由于实际流体的粘性,使得流体运动的研究变得非常复杂。为了便于理论分析,在流体力学中引进了“理想流体”的概念。理想流体就是没有粘性的流体,当然这是一种假想的流体,实际中并不存在。但研究无粘流体的运动,可以使问题大大简化,容易得到流体运动的基本规律。

对某些粘性影响不大的流动问题,忽略粘性所得到的结果与实际结果往往差别不大。而对于必须考虑粘性作用的流动问题,除了使用更典型的有粘方法,也可专门对粘性作用进行分析,然后再对理想流体的结果进行修正和补充。
牛顿流体 VS 非牛顿流体
那么流体的粘性和什么有关呢?
作为世界物理学界Top2的男人,牛顿除了被苹果砸到,发现各种牛X定理,霸屏整个中学物理课本之外,连流体也不肯放过。经过大量的实验研究,牛顿于1686年提出了著名的“牛顿内摩擦定律”——流体的内摩擦力(即粘性力)的大小与流体的性质(粘性系数μ)有关,并与流体的速度梯度和接触面积成正比。

大量实验证明:大多数气体、水和许多润滑油都能很好的遵循上述的牛顿内摩擦定律,即当压力和温度一定时,流体的内摩擦应力与速度梯度成正比。这种满足牛顿内摩擦定率的流体称为牛顿流体。需要指出的是,尽管我们平时接触到的大部分流体都是牛顿流体,仍有一些流体比如生物流体、高分子聚合物的浓溶液等,不能遵循牛顿内摩擦流体,称为非牛顿流体。
连续介质 VS 非连续介质
我们知道,N-S方程描述了基于连续介质假定的牛顿流体的动量守恒。“连续”是一个比较直观的概念——“剪不断,理还乱”,正如我们宏观所见的流体。不过在流体力学层面,有一个无量纲数可以作为衡量连续与否的标识——这便是努森数(Kn),其定义为分子平均自由程长度与典型的物理尺度之比。

基于努森数的定义可以知道,努森数越大,意味着物理尺度和分子平均自由程越接近,分子的离散效应越强,研究中越不能忽略分子之间复杂的作用力;反之,努森数很小,意味着物理尺度远远大于分子自由程,不再关注分子团内部的相互作用,转而研究其宏观状态的密度、速度、压力等参量。
下图给出了基于努森数定义的流体状态,其中Kn小于0.001,则认为流体满足连续介质的假设。常温常压下的分子平均自由程约为70nm,由此可以估算自然环境下,0.07mm的物理尺度即可满足连续介质假设,因此工程上绝大部分的流动问题都可以认为是连续流体,满足N-S方程的前提条件。

对于努森数足够大的流体,比如极稀薄气体,可以直接使用分子动力学进行描述,利用汉密尔顿方程求解。而二者之间还有滑移流体和过渡流体等不同的类别,分别对应有专门的描述方法。
热动平衡 VS 非热动平衡
除了上面提到的牛顿流体、连续介质假定两个前提条件,N-S方程还有一个局限——它只适用于大尺度的缓变行为,也是我们通常所说的“热动平衡”或“准热动平衡”的状态,此时分子的热动松弛时间(恢复到局部热动平衡的时间)远远小于宏观尺度。现实中大部分流动问题都属于这两类。而非热动平衡状态,比如冲击、爆炸等,宏观流动的特征时间也极短——以至于分子的热动松弛不可被忽略。

欧拉法 VS 拉格朗日法
说完了实质,再看看形式——流体力学的两种主要描述方式:拉格朗日法和欧拉法。
在经典场论中,拉格朗日法(又称体系法)是研究流场内个别流体质点在不同时刻的位置、流速、压力等参数的变化。也就是用随时间的变化来描述流体质点的运动参数,各质点运动状况的总和就构成了整个流体的状态。
欧拉法(又称控制体法)是研究整个流场内不同时刻,不同位置上的流体质点的参数。它把注意力集中在选定的空间点上而不是选定的流体质点上。因此,欧拉法确定的是占据流场中的全部流体质点的瞬时流动参数。

为了更形象的对比欧拉法和拉格朗日法,小编整理了上面这幅图:拉格朗日法就好像是跟在鸭子后面划船,而欧拉法则更像是在站在桥上数多少鸭子游过去。需要特别说明的是,最早提出这两类研究流体方法的人都是欧拉。
N-S方程 VS 玻尔兹曼方程
前面铺垫了这么多,目的还是把玻尔兹曼这尊大神娓娓的请出来。当然在此之前,还有必要先来捋一捋经典力学描述流体的方式。
流体的基本方程本质上是质量、动量和能量守恒方程,而N-S方程只是在宏观上基于连续介质假定,利用偏微分方程描述粘性流体流动的运动方程,仅仅是流体基本方程的一种表达方式。而N-S方程反映的就是牛二定律F=ma。我们先来回顾一下用欧拉法描述的N-S方程的推导过程:

除了上述的动量方程之外,我们同样可以推导微分形式的质量和能量守恒方程,此处不再赘述。而反观另外一种描述流体运动的玻尔兹曼方程,则会看到一种完全不同的奥妙。
1859年,麦克斯韦发现在宏观系统中追踪每个分子的运动轨迹难以实现,于是产生了统计平均的概念。麦克斯韦认为,任意时刻单个分子的速度和位置信息并不重要,分布函数才是描述分子效应的重要参数。速度分布函数给出了在某一给定时间,速度在一定范围内的分子在整个系统中所占的百分比。当气体处于热动平衡状态时,气体将均匀的分布,而唯一的未知量就是速度分布函数。

这种方法并非直接描述流体的速度、压力等宏观变量,也非直接描述每个流体分子的微观运动,而是用统计的方法描述空间内流体粒子的速度分布。其描述方式介于宏观和微观之间,被称之为介观。玻尔兹曼更进一步将麦克斯韦分布推广到任意大系统,他第一个认识到熵的热力学概念和大系统状态的统计分析之间的紧密联系,即宏观变量中系统的熵随着时间增大,与微观分子排列的最大可能数相对应。
听不懂,听不懂,听不懂,说人话!
老话说:不患寡而患不均,不均就会出问题,打土豪啊分田地。
任意大系统虽然不像麦克斯韦的描述那么平均,但会趋向于平均。比如我们用活塞将盒子内的分子都压到一侧,松开活塞后,分子将迅速扩展到整个盒子空间并趋于均匀分布。
对于这样的过程需要有更详细的数学描述。于是,玻尔兹曼输运方程及其质量、动量和能量守恒方程便呼之欲出了。通过这些方程先求解出粒子的介观分布,进而可推导出宏观属性。

至此,我们可以对玻尔兹曼眼中的流体力学做个总结:使用拉格朗日方法观察处于介观尺度下的流体粒子的分布规律,并使用统计学思路研究其输运与守恒,并通过积分将介观的速度分布函数和宏观的物理量建立联系。

也许,很少有人关注细小砂砾的运动,而它恰恰是形成各种复杂山体结构的本源。如果说传统CFD方法是“通过外表看现象”,那么LBM方法则更像是“通过本质看现象”。
N-S方程的数值方法 VS LBM
无论是N-S方程还是玻尔兹曼方程,都是描述流体运动的解析方法。面对实际问题复杂的边界和初始条件,最终还是要回归到离散求解的数值方法。
对于N-S方程的数值求解,最常规的有限体积法(FVM)的思路就是在流体域的每个离散控制体网格上分别施加方程进行求解;格子玻尔兹曼方法(LBM)同样也是在格子上对玻尔兹曼方程进行时空的离散,只是对付这个简单的线性方程,其数学处理要简单的多。

当然,无论是LBM还是N-S数值方法的构建,都是可以看成对最基本的大量微观粒子运动的合理粗化。如果只在离散的格子内研究其速度分布函数,并将粒子的运动简化为只沿有限个特定的方向,则演化为LBM;而基于连续的牛顿流体和近热动平衡的假设,在有限的单元内研究流体的宏观参数,则演化为N-S方程的数值方法。
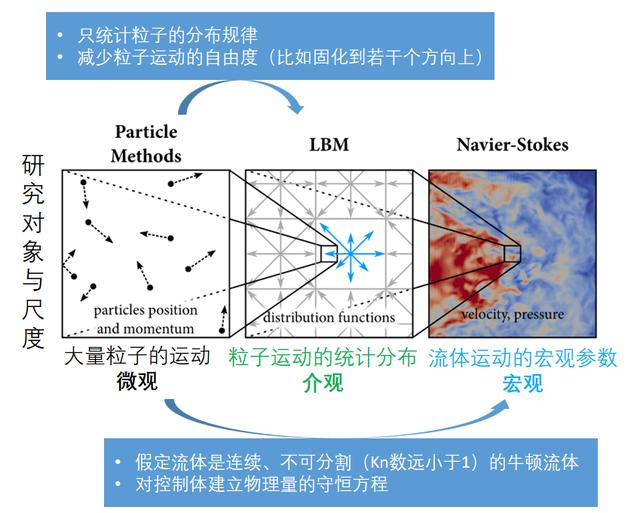
两种数值方法主要区别见下表,可见这是两套完全不同的思路和实现方法。LBM虽是求解粒子的速度分布,形式上是一种统计的方法,但其本质上仍是追踪离散粒子的运动,最终获取整个流场的粒子状态,是一种比N-S方程更接近物理本质的描述。

国内外有很多学者专注于LBM方法,但研究大多集中在多相流或者稀薄气体等传统CFD软件很难模拟的领域。事实上许多学者为了向世人证明LBM并不是天马行空的猜想,使用严格的数学推导,基于LBM方程施加Kn数远小于1的假设条件,推导出了N-S方程。因此可以认为,N-S方程的描述是LBM在连续介质条件下的一个特例,而玻尔兹曼则为世人提供了一个更为接近物理本源的恢弘视角看待流体。
所以,LBM方法在传统CFD的研究领域一样拥有独特的优势,比如汽车和飞机的空气动力学与气动噪声问题。或许这也可以给学者们在选择LBM的应用领域上提供一些启发和参考吧。
流体力学从入门到放弃,大概只需要一杯咖啡的时间。至此,相信小伙伴们可以放心大胆的向领导回复:“领导,饮水机在哪?要不要给您泡点茶叶?”
-END-
来源:LBM与流体力学
原标题:玻尔兹曼眼中的流体力学
编辑:fiufiu