基于BDS/UWB的协同车辆定位方法
徐爱功,曹楠,隋心,王长强,高嵩
辽宁工程技术大学 测绘与地理科学学院
摘要
针对当前协同车辆定位精度低以及城市复杂环境下协同车辆定位精度不可靠等问题,该文提出一种在车车通信环境下利用BDS/UWB组合系统进行协同车辆定位的算法。该算法综合利用BDS在城市复杂环境下的定位优势、UWB具有可同时提供短程无线通信功能和高精度测距观测值特性,通过扩展卡尔曼滤波对BDS双差观测信息和UWB测距信息进行融合,从而实现高精度、高可靠性协同车辆定位。实验结果表明:BDS/UWB组合系统在较好观测环境下定位精度可达厘米级,在复杂环境下定位精度可达分米级;相比于BDS单系统,BDS/UWB组合系统在较好观测环境下定位精度提升并不明显,平均提升了1.49 cm,但在复杂环境下定位精度平均提升6.88 cm,定位可靠性较单BDS系统也有明显改善。
本
文
目
录
0 引言
1 BDS/UWB协同定位方法
2 实验与分析
3 结束语
0
引言
随着现代车联网和智能驾驶系统的发展,基于车车(vehicle-to-vehicle,V2V)无线信息交互的协同定位方案受到了各国学者的关注。依靠V2V通信技术,车辆之间可以实现车载传感器的运动状态信息以及位置信息的实时交互,通过V2V的相对位置解算,可以获得准确可靠的定位结果。对比OEM预埋系统,基于V2V通信技术下的多传感器信息融合协同车辆定位方案在车道偏离、自适应巡航控制和盲点侦测等方面发挥更多的作用,也为主动交通安全提供了新的解决方案[1-2]。
随着我国北斗卫星导航系统(BeiDou navigation satellite system,BDS)的不断完善与建设,BDS逐渐成为交通领域的主要定位技术之一。BDS的卫星星座构成同时包括地球同步轨道(geosynchronous earth orbit,GEO)、倾斜地球同步轨道(inclined geosynchronous orbits,IGSO)和中地球轨道(medium earth orbit,MEO)卫星[3]。相比于只包括MEO卫星星座的GPS、GLONASS和Galileo,BDS能在中国及周边区域,保证在天顶方向具有相对多的观测卫星,这对于城市复杂观测环境下的车辆高精度定位是有益的[4]。然而在一些特殊情况下,例如城市峡谷,GNSS卫星信号遭受严重的遮挡、衰减和多径干扰等因素影响,定位精度急剧下降,甚至无法定位,单独依靠GNSS无法完全满足智能驾驶系统对车辆定位精度的要求[5]。针对这一问题,研究人员提出多种优化方案,包括惯性导航[6-7]、视觉传感器和三维激光扫描技术等[8-9],但这些方案中难以对系统复杂度、成本和定位精度等因素进行平衡优化,定位结果精度与协同车辆定位的实际需求存在一定的差距。
WiFi、蓝牙、超宽带(ultrawide band,UWB)等专用短程无线通信(dedicated short-range communication,DSRC)技术可以为多个车辆单元节点之间构成的共享信息网络提供重要纽带,同时也具有定位辅助功能[10]。WiFi技术在正常环境中可以达到米级定位的精度,但在复杂环境中,WiFi信号易于受到其他信号影响,定位精度下降明显,且能耗较高,实用性降低。蓝牙技术所需设备体积小,功耗低,易于集成到终端设备上,且传输不受视距影响,但在复杂环境中稳定性较差,易受噪声干扰。早期文献[11]将WiFi与GPS组合,设计了一种松耦合模式下的车辆协同定位方案,定位结果精度可达1.38 m,但该定位精度无法满足协同车辆定位中分米级甚至厘米级的定位精度要求。相比于WiFi和蓝牙技术,UWB无线定位技术具有抗多径和抑制信号反射的能力,测距精度可达厘米级,可以为V2V提供高性能的测距通信服务[12]。文献[13-14]利用最小二乘方法对UWB定位精度进行评估,实验结果表明:在GPS不能提供定位信息情况下,UWB可为动态车辆提供分米级定位,但该方法采用传统的距离交会法进行定位,未对移动车辆之间的协同定位进行分析和探讨。文献[15]针对协同车辆定位中GPS与UWB两类传感器观测噪声差异对定位结果精度产生一定影响偏差的问题,提出一种先削弱偏差再利用GPS伪距观测值与UWB测距值融合的定位算法,实验得到40 cm的组合定位精度,但该算法仅仅使用到了GPS的伪距观测值,同时实验验证时也并未对可视卫星数减少的复杂情况进行考虑。文献[16]通过对车辆运动的连续性和定位信息的不确定性等问题的研究,提出了一种GPS与前置距离传感器组合的协同定位算法,通过数据融合解算的定位,结果平均定位误差为0.85 m,比传统的自车导航精度提高35.2%,可靠性提高42.6%,但该算法只在仿真实验中进行了验证,缺少实车数据的算法完善。
基于以上分析可以认为,将GNSS与DSRC进行组合,能够提高车辆间短距离导航信息的连续性和抗干扰能力,增强协同车辆定位的精度。相对于GPS、BDS在复杂城市环境下进行高精度定位更具优势;相对于WiFi和蓝牙,UWB无论在通信和测距方面都有更好的表现。因此本文提出一种基于BDS/UWB组合的协同车辆定位方法,通过对BDS观测方程进行构建,采用UWB距离观测值对车辆间基线长度进行约束,形成BDS/UWB组合观测方程,利用扩展卡尔曼滤波器(extended Kalman filter,EKF)进行位置参数解算,最终获得高精度的协同车辆定位结果。
1 BDS/UWB协同定位方法
1.1 BDS双差观测方程
假设1台GNSS接收机a接收到BDS卫星B1的观测信息,则顾及卫星、接收机和信号传播延迟等误差的伪距和相位原始观测方程分别为:
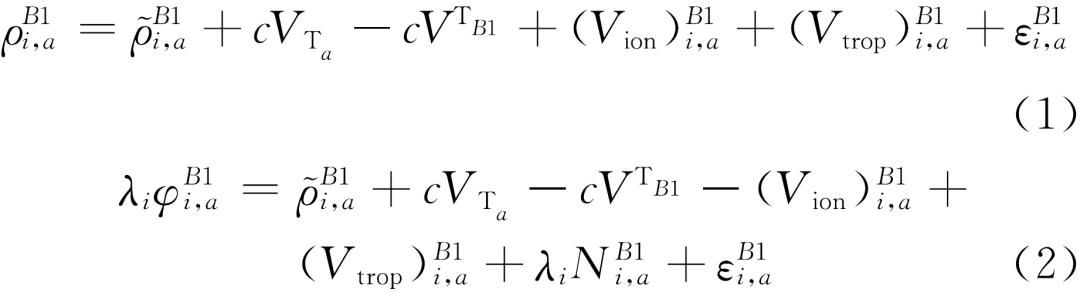
式中:i、ρB1i,a和φB1i,a分别为测站a对于卫星B1的载波观测频率、伪距观测值和相位观测值;λi为i载频波长;B1i,a为接收机到卫星的几何位置;c为光速;VTa为接收机钟差;VTB1为B1卫星钟差;N为模糊度;Vion和Vtrop分别为电离层延迟和对流层延迟;εB1i,a为其他观测值噪声。
在2台GNSS接收机a和b间求单差,可以消除BDS卫星的时钟误差。BDS站间单差方程可以表示为:


车辆协同定位过程中,车与车之间的距离较短,因此在BDS数据处理过程中电离层和对流层延迟可以不予考虑[17],即(ΔVion)B1i,ab=0,(ΔVtrop)B1i,ab=0。
分别对单差观测式(3)和式(4)进行BDS卫星B1和B2间求差,可以消除接收机钟差,得到BDS双差观测方程为:

1.2 UWB测距观测方程
目前UWB的测距技术有多种,本文使用的基于双向到达时间(two-way time of arrival,TW-TOA)测距,该测距技术无须增加硬件成本,降低实现复杂程度,不需要UWB测量单元间的时间同步,可以间接获取精度较好的测量距离[18]。
UWB测距过程中流动站与基站间存在固定时间附加延时以及环境中温度和湿度等因素造成的误差TD,同时TW-TOA测距过程也会引入设备响应延迟时间Trespond[19],将这两类误差统称为设备标准时间偏差TSD,模型表示为:

式中:Tround表示信号双向传递所用时间;la为UWB测距单元a发射脉冲信号的位置;lb为UWB测距单元b接收脉冲信号的位置;c′为脉冲信号传播速度。
所以,两个车载UWB测距单元a和b之间的TW-TOA测距观测方程为:
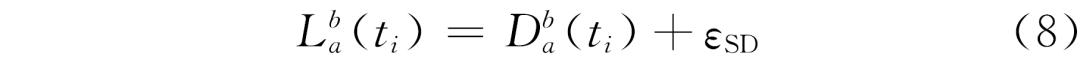
式中:Lba(ti)为ti时刻两个UWB测距单元a和b之间的真实距离;Dba(ti)为测距值;εSD为标准偏差。
为消除标准时间偏差影响,在视距(line of sight,LOS)环境下,通过大量的测距信息平均值与测距信息真实值间的差值算出ε,最后拟合确定出标准时间偏差的误差模型,具体方法见参考文献[20]。
对BDS双差观测方程进行解算,可获得车辆间基线信息,而UWB可直接对车辆间基线距离进行精确观测,因此可将UWB的测距值加入BDS双差观测方程中,对基线长度进行约束,该方法理论上可提高复杂观测环境下的基线解算精度。UWB约束条件方程可表示为:

式中:ρUba为消除标准时间偏差后的UWB测距值;ρBba为基线距离;ε为其他观测值噪声。
1.3 BDS/UWB协同定位模型
利用BDS/UWB组合系统,在UWB通信范围内移动平台间可实时相互传输BDS导航电文、载波相位和伪距等信息,同时UWB与其他移动平台间相互测距,将UWB高精度测距信息与从周围移动平台获得的BDS观测信息进行融合,实时解算出移动平台间三维基线向量。BDS/UWB协同定位原理如图1所示,将进行信息融合的移动平台称为目标车辆,将与目标车辆保持车车通信测距的移动平台称为信息传输车辆。

图1 BDS/UWB协同定位原理示意图
BDS/UWB协同定位方法流程如图2所示。目标车辆的概略坐标由伪距单点定位得到。信息传输车辆运动过程中BDS/UWB组合单元的初始坐标和运动速度由BDS获取的伪距单点定位和多普勒频移数据实时解算获取,再由上一历元的瞬时位置坐标和运动速度计算出下一历元的瞬时位置,公式为:

式中:(Xi,Yi,Zi)和(νX,νY,νZ)为上一历元的瞬时位置和速度;(Xi 1,Yi 1,Zi 1)为下一历元的瞬时位置;tage为两次历元的间隔时间。

图2 BDS/UWB协同定位方法流程图
本文利用计算量较小的EKF滤波进行参数估计,其核心思想为:对非线性系统观测方程进行泰勒级数展开,并略去二阶及以上项,得到一个近似的线性化模型,然后利用线性卡尔曼滤波完成对目标的滤波估计[21]。
对式(5)、式(6)和式(9)进行线性化推导,可得:


式中:mB1i,a、mB2i,a、nB1i,a、nB2i,a、lB1i,a和lB2i,a分别为测站近似位置到卫星方向上的方向余弦;mUa、nUa和lUa分别为测站a近似位置到测站b的方向余弦;dX、dY和dZ表示位置参数;εba为测量噪声。
选择BDS卫星B1为参考卫星,根据上文公式可推导得到BDS/UWB线性化后的观测模型为:

式中:Zk为观测信息;Hk是量测矩阵;Xk表示状态向量;R为观测噪声项。

BDS/UWB线性化后的状态模型为:


维数与状态向量相同;ωk为第k时刻的激励噪声项。
由于2种传感器观测精度不同,需要对不同传感器接收到的观测值进行定权[22]。采用经验值定权方法在多数情况下不够精确,无法满足本文在复杂环境下的数据成果要求,因此必须要选择一种有效的数学方法应用于BDS/UWB组合系统。本文采用的是赫尔默特方差估计方法进行定权[23]。
由上述推导得到的式(13)和式(14)进入卡尔曼滤波器递推过程为:

式中:k和k为k时刻状态量的滤波值和预测值;k和k为k时刻误差协方差矩阵的滤波值和预测值;Kk 1为k 1时刻滤波增益矩阵。
利用EKF滤波器进行参数解算,模糊度此时为浮点值,利用LAMBDA方法进行模糊度固定[24],最终获得高精度的协同车辆定位结果。
2 实验与分析
为了对本文所提方法的协同定位性能进行验证,在辽宁工程技术大学玉龙校区的内部道路中进行了实验测试,移动定位平台如图3所示。平台包括:Leica GS14 GNSS接收机、Time Domain P440 UWB模块、MP-POS510 GNSS/INS组合定位定姿系统。其中:GS14 GNSS接收机和P440 UWB模块用来提供BDS和UWB原始观测数据;P440 UWB模块理论测距值为410 m,通过实际测试,对100 m距离内的测距值进行了有效标定,能够达到厘米级定位精度;MP-POS510为本次实验提供车辆运动过程中的参考位置,其精度指标见表1。

图3 移动定位平台
表1 MP-POS510精度指标

为模拟车辆行驶过程中的V2V的真实相对位置关系,实验中对移动平台之间相对运动关系设计了2种方案。方案1是在BDS观测条件较好环境下,固定2个移动平台的相对距离并使平台按照规划的轨迹运行,如图4(a)所示;方案2是解除方案1中对移动平台间的距离约束,更加接近真实车辆行驶中与周围其他车辆的相对位置关系,同时增加弱GNSS信号区域下的V2V实验,运行轨迹如图4(b)所示。

图4 运行轨迹示意图
BDS/UWB组合系统中的2种传感器具有不同的时间和坐标系统,需要将两者的时间系统进行统一,并将解算结果归算到同一坐标系下[25]。通过BDS实时伪距单点定位解算的接收机钟差改正数获得高精度接收机钟时间,利用软件对电脑进行授时,从而保证接收到的UWB测距数据和BDS原始观测数据在时间系统上保持一致。通过对UWB的采样率进行控制,将BDS与UWB观测时刻相对应,使得2种观测数据在采样历元上相匹配。实验中,移动平台的行进速度大约为5 (m·s-1),设定UWB和BDS的采用时间间隔为1 s,设定GS14 GNSS接收机观测截止角为10°。
2.1 固定基线长度V2V测距实验
方案1中,目标移动平台上BDS的可视卫星数和位置精度因子(position dilution of precision,PDOP)值如图5所示。BDS可视卫星有5~7颗,大部分时段的PDOP值小于3,观测条件较好。

图5 观测BDS卫星数量和PDOP值
图6(a)为BDS/UWB组合系统和单BDS系统基线解算结果偏差,实验中固定2个移动平台间基线长度为5.215 m。图6(b)为BDS/UWB组合系统相对定位中的RATIO值变化情况。在较好观测条件下,BDS/UWB组合解算的结果中有86.7%的RATIO值大于3,模糊度能够固定,BDS/UWB组合系统基线解算结果最大误差为12.69 cm,最小误差为2.93 cm,平均精度8.76 cm,标准偏差(standard deviation,STD)值为2.39 cm;单BDS系统基线解算结果最大误差为13.75 cm,最小误差为6.02 cm,平均精度为9.82 cm,STD值为2.46 cm;BDS/UWB组合系统基线解算结果偏差分布相比单BDS系统更加集中,误差值较小,精度平均提高1.06 cm。

图6 基线解算结果偏差和RATIO值
表2为各个系统的均方根误差(root mean square error,RMSE)。从表2中看出,在东向(E)和天向(U)上,BDS/UWB组合系统基线解算的RMSE均小于单系统的RMSE值,北向(N)两者精度相当。
表2 BDS/UWB组合系统基线解算精度统计

2.2 变基线长度V2V测距实验
方案2中,实验分别在BDS可视条件较好和复杂两种环境中进行,实验以MP-POS510设备解算结果作为参考检核值。在复杂环境中,目标移动平台行驶经过高层建筑物密集、天顶方向存在部分遮挡的路段。在图7(a)和图7(b)为可视条件较好环境下BDS可视卫星数和PDOP值随时间变化情况,可视卫星数为7~8颗,整个时段PDOP值均小于3。图7(c)和图7(d)为复杂环境下BDS可视卫星数和PDOP值情况,部分时段可视卫星数最小值为2颗,PDOP值最大为17.6。


图7 两种环境下观测BDS卫星数量和PDOP值
图8为2个系统在较好环境下基线解算结果偏差和RATIO值。BDS/UWB组合解算的结果中有91.3%的RATIO值大于3,模糊度能够固定。通过与参考检核值进行比较,BDS/UWB组合系统基线解算结果最大误差22.15 cm,最小误差1.09 cm,平均精度12.62 cm,STD值为5.59 cm;单BDS系统基线解算结果最大误差24.41 cm,最小误差3.26 cm,平均精度14.55 cm,STD值为5.77 cm;BDS/UWB组合系统基线解算结果相较于单BDS系统更接近于参考系统的检核值,精度平均提高1.93 cm。
图9为在复杂环境下误差与RATIO值指标情况。由于可视卫星数少及周边环境较差,BDS/UWB组合解算的RATIO值多在3附近波动,局部时段低于1,模糊度不易固定。BDS/UWB组合系统基线解算结果最大误差187.94 cm,最小误差0.01 cm,平均精度28.55 cm,STD值为47.71 cm;单BDS系统基线解算结果最大误差191.62 cm,最小误差0.02 cm,平均精度35.43 cm,STD值为52.02 cm;BDS/UWB组合系统和单BDS系统基线解算结果均与参考检核值差距较大,但组合系统误差略小,精度平均提高6.88 cm。
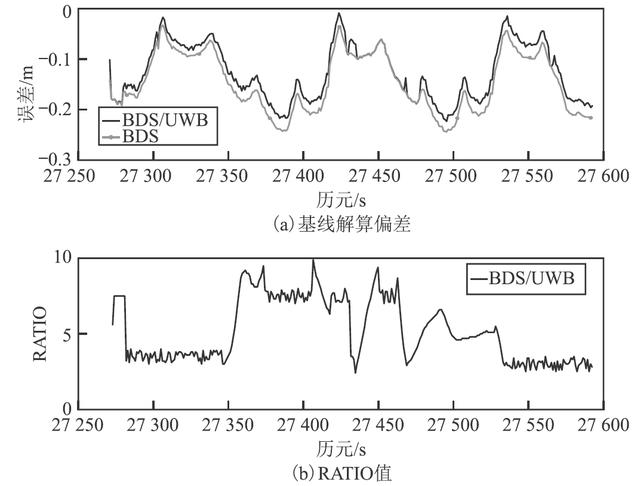
图8 较好环境下基线解算结果误差和RATIO值

图9 复杂环境下基线解算结果误差和RATIO值
表3和表4为各个系统在两种环境下的RMSE值。从2个表中可以看出,BDS/UWB组合系统基线解算的RMSE值均小于单BDS系统基线解算的RMSE值。当移动平台所处环境复杂时,BDS/UWB组合系统与单BDS系统的RMSE值均明显变大,基线解算结果精度下降。
由于实验条件限制,处在复杂环境中的实验移动定位平台之间出现过短暂的UWB非视距状态,BDS/UWB组合系统相较单BDS系统基线解算结果精度提升并不明显,如图9中历元 28 350 s附近所示,UWB非视距状态对组合系统定位精度提升产生了一定影响。同时,由于平台移动有轻微震动的情况,未能严格按照规划的轨迹运行,存在2 cm左右的误差。这些因素导致所求解的BDS/UWB组合的协同定位精度与理想环境下求解的BDS/UWB组合定位精度存有偏差。
表3 较好环境下BDS/UWB组合系统基线解算精度统计表

表4 复杂环境下BDS/UWB组合系统基线解算精度统计表

3 结束语
为了有效提高城市峡谷中车辆之间相对定位精度及可靠性,本文提出一种基于BDS/UWB的协同车辆定位方法。该方法综合利用BDS在城市复杂环境下的定位优势、UWB具有可同时提供短程无线通信功能和高精度测距观测值特性,将车辆之间观测信息进行数据融合解算,最终实现复杂环境下高精度车辆协同定位。实验结果表明:BDS/UWB组合系统的基线解算结果优于BDS单系统基线解算结果。相较于BDS单系统,在较好观测环境下组合系统定位精度平均提升1.49 cm,在复杂环境下组合系统定位精度平均提升6.88 cm,BDS/UWB组合系统的基线测量精度和可靠性较BDS单系统有明显改善。因实验设备和场地限制,现阶段难以对所有协同车辆定位的场景进行模拟实验,这对BDS/UWB组合系统的可靠程度存在一定影响。在后续的研究中,将会增加多种实验场景并将UWB组网定位数据与BDS数据进行融合,进一步提高协同车辆定位的稳定性和精度。
参考文献(略)
END
作者简介:徐爱功(1963—),男,山东日照人,教授,博士,主要研究方向为全球卫星定位系统、地理信息系统及智能交通系统的集成与应用。
E-mail:Xuaigong@lntu.edu.cn
基金项目:国家重点研发计划项目(2016YFC0803102);辽宁省教育厅辽宁省高等学校基本科研项目(LJ2017QL007)
通信作者:曹楠 硕士研究生 E-mail:c_nan@qq.com
引用格式:徐爱功,曹楠,隋心,等.基于BDS/UWB的协同车辆定位方法[J].测绘科学,2020,45(6):1-8.(XU Aigong,CAO Nan,SUI Xin,et al.Cooperative vehicle positioning method based on BDS/UWB[J]. Science of Surveying and Mapping,2020,45(6):1-8.)